ローレンツ因子というものがある。
このローレンツ因子とは、「動いている物体」をどこから見たかにより、
「動いている物体」と自分自身にどれくらい時間のずれや尺度のずれが生じるのかを
表現したもの。
この因子を求める方法に関して、具体的に書くと以下の通り。
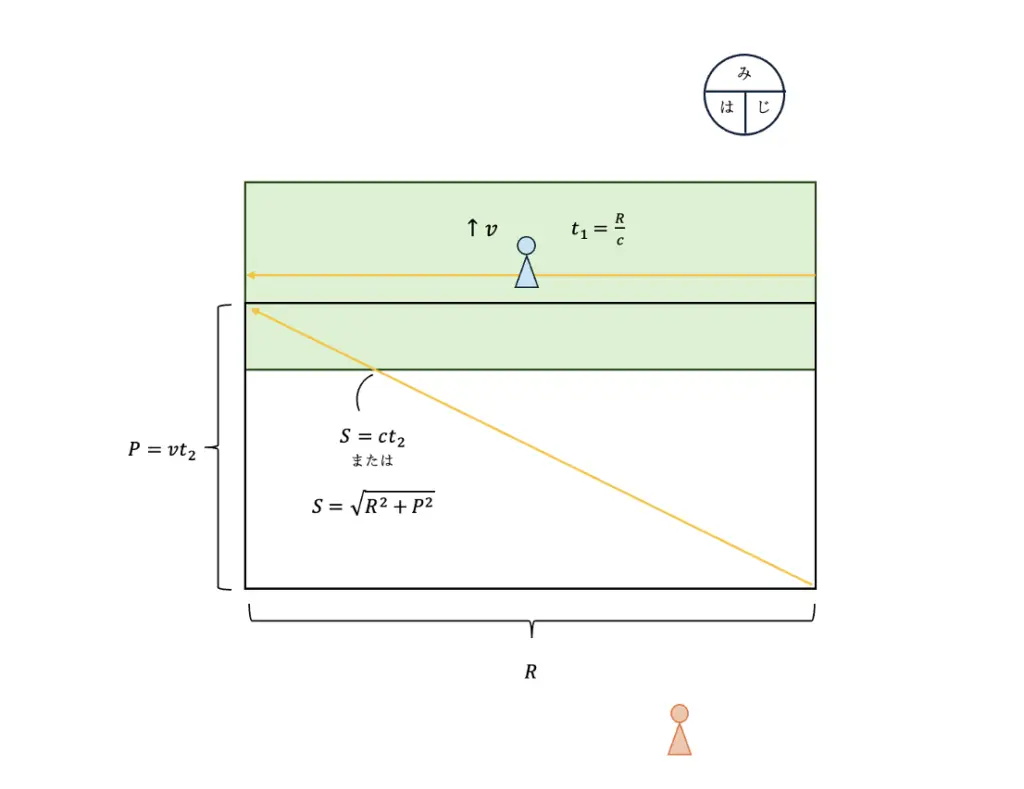

この時、ローレンツ因子を求めるにあたり比較したいのは、$t_1$ と$t_2$。
何故なら、$t_1$と$t_2$にずれが生じる可能性があるため。
ずれが生じるとするならば、どれくらいのずれが生じるのか。。。
それを求めるために、$\dfrac{t_2}{t_1}$ を計算してみよう。
何故、$\dfrac{t_2}{t_1}$を求めるのか?
それは、$t_1$(基準になる値) に対して$t_2$が何倍になっているかを知るため。
つまり、$\dfrac{t_2}{t_1}$を求める事で $t_1$(基準になる値)に対して
$t_2$がどれくらい間隔的にずれているのかが分かる。
今、$t_1$を分母(基準)にとった理由は、
自分自身にとって自分自身とは常に静止した存在であるから。
つまり、(自分自身から見た時に)動いている人物に生じる時間を基準にとるよりは、
(自分自身から見た時に)静止している人物に生じる時間を基準にとった方が
「自分自身にとって生じる時間」を基準とした比較ができるため。
では、実際に計算してみよう。
上の図を利用すると、
三平方の定理より
$S=\sqrt{R^2+P^2}$ __①
また、$S=ct_2$ __② とも表せ
①に②を代入すると
$ct_2=\sqrt{R^2+P^2}$ __③
この時 $t_1=\dfrac{R}{c}$であることより
∴ $ct_1=R$ __④
また、$P=vt_2$ __⑤
③に④、⑤を代入して
$ct_2=\sqrt{(ct_1)^2+(vt_2)^2}$
$ct_2=\sqrt{c^2t_1^2+v^2t_2^2}$
両辺を2乗して
$c^2t_2^2=c^2t_1^2+v^2t_2^2$
従って
$c^2t_2^2-v^2t_2^2=c^2t_1^2$
$(c^2-v^2)t_2^2=c^2t_1^2$
$\cfrac{(c^2-v^2)t_2^2}{t_1^2}=c^2$
$\cfrac{t_2^2}{t_1^2}=\cfrac{c^2}{c^2-v^2}$
$\cfrac{t_2^2}{t_1^2}=\cfrac{1}{\cfrac{c^2}{c^2}-\cfrac{v^2}{c^2}}$
$\cfrac{t_2^2}{t_1^2}=\cfrac{1}{1-\cfrac{v^2}{c^2}}$
この時
$\cfrac{t_2}{t_1}=\pm{\displaystyle\sqrt{\cfrac{1}{1-\cfrac{v^2}{c^2}}}}$
また $\cfrac{t_2}{t_1}>0$より
$\cfrac{t_2}{t_1}=\displaystyle\sqrt{\cfrac{1}{1-\cfrac{v^2}{c^2}}}$
従って、
$\cfrac{t_2}{t_1}=\cfrac{1}{\sqrt{1-\cfrac{v^2}{c^2}}}$
これが、「ローレンツ因子」と呼ばれるもの。
この3年間で、私が少し考えたのは、
このローレンツ因子を拡張できないかという事。
Cはどこから見てもCだとするならば、
2C、3C、4Cという値もどこから見ても2C、3C、4Cであるはずで
という事は2Cを基準にとってローレンツ因子の拡張が出来ないだろうか?
イメージ図を下に記す。
※ただ、Cを2Cに変えただけ(速度の範囲は $c\leq{v}<2c$)。
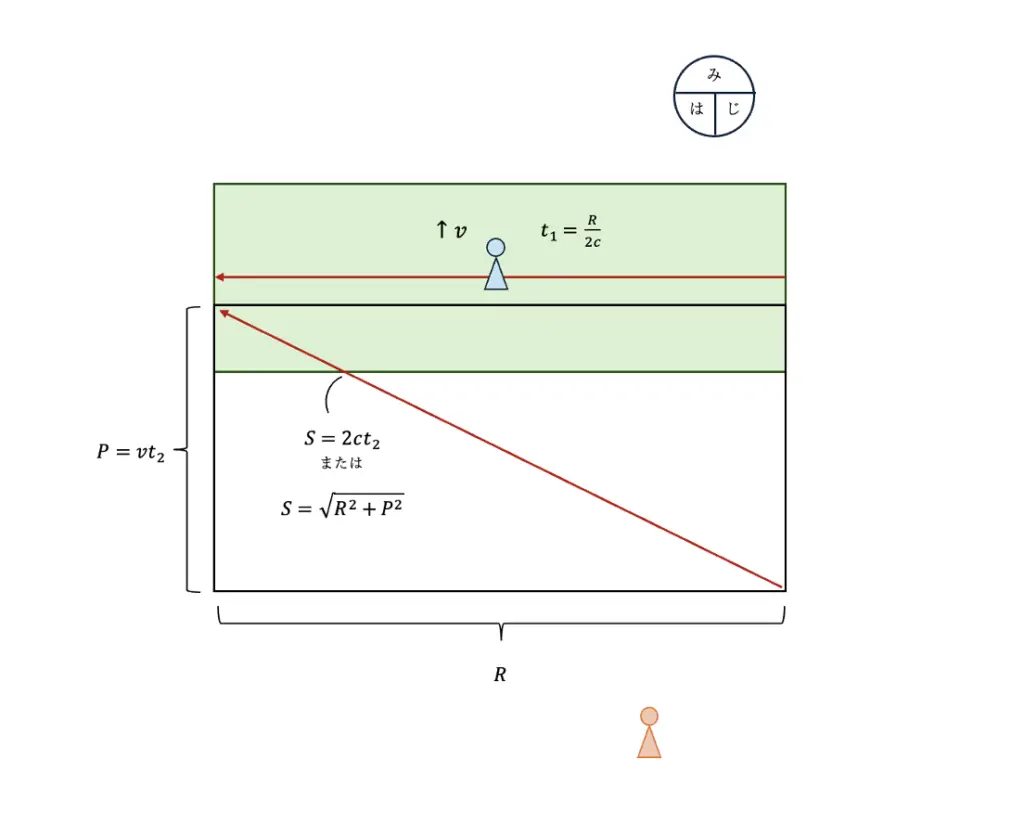
具体的に計算すると、
三平方の定理より
$S=\sqrt{R^2+P^2}$ __①
また、$S=2ct_2$ __② とも表せ
①に②を代入すると
$2ct_2=\sqrt{R^2+P^2}$ __③
この時 $t_1=\cfrac{R}{2c}$ であることより
$2ct_1=R$
∴ $R=2ct_1$ __④
また $P=vt_2$ __⑤
③に④、⑤を代入して
$2ct_2=\sqrt{(2ct_1)^2+(vt_2)^2}$
$2ct_2=\sqrt{4c^2t_1^2+v^2t_2^2}$
両辺を2乗して
$4c^2t_2^2=4c^2t_1^2+v^2t_2^2$
従って
$4c^2t_2^2-v^2t_2^2=4c^2t_1^2$
$(4c^2-v^2)t_2^2=4c^2t_1^2$
$\cfrac{(4c^2-v^2)t_2^2}{t_1^2}=4c^2$
$\cfrac{t_2^2}{t_1^2}=\cfrac{4c^2}{4c^2-v^2}$
$\cfrac{t_2^2}{t_1^2}=\cfrac{1}{\cfrac{4c^2}{4c^2}-\cfrac{v^2}{4c^2}}$
$\cfrac{t_2^2}{t_1^2}=\cfrac{1}{1-\cfrac{v^2}{4c^2}}$
この時
$\cfrac{t_2}{t_1}=\pm{\displaystyle\sqrt{\cfrac{1}{1-\cfrac{v^2}{4c^2}}}}$
また $\cfrac{t_2}{t_1}>0$より
$\cfrac{t_2}{t_1}=\displaystyle\sqrt{\cfrac{1}{1-\cfrac{v^2}{4c^2}}}$
従って、
$\cfrac{t_2}{t_1}=\cfrac{1}{\displaystyle\sqrt{1-\cfrac{v^2}{4c^2}}}$
これで、「ローレンツ因子の拡張」が出来た。
従って、特殊相対性理論と同様の導出方法で
$x_B^\prime=\cfrac{x_B-v_Bt}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}$ $x_B=\cfrac{x_B^\prime+v_Bt_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}$
$t_B^\prime=\cfrac{t-\cfrac{v_B}{4c^2}x_B}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}$ $t=\cfrac{t_B^\prime+\cfrac{v_B}{4c^2}x_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}$
ただし、$c\leq{v_B}<2c$と導ける。
ただ、$c\leq{v_B}<2c$で飛んでいる物質は存在しないのだけれど(笑。
ちなみに、特殊相対性理論の方程式はこんな感じ。。。
$x_A^\prime=\cfrac{x_A-v_At}{\sqrt{1-\cfrac{v_A^2}{c^2}}}$ $x_A=\cfrac{x_A^\prime+v_At_A^\prime}{\sqrt{1-\cfrac{v_A^2}{c^2}}}$
$t_A^\prime=\cfrac{t-\cfrac{v_A}{c^2}x_A}{\sqrt{1-\cfrac{v_A^2}{c^2}}}$ $t=\cfrac{t_A^\prime+\cfrac{v_A}{c^2}x_A^\prime}{\sqrt{1-\cfrac{v_A^2}{c^2}}}$
ただし、$0\leq{v_A}<c$
今、$x_A$、$x_A^\prime$、$x_B$、$x_B^\prime$、$t$、$t_A^\prime$、$t_B^\prime$と置いたのには、ちょっとした理由がある。
後に、その種明かしをしようと思う。


