次の疑問は、「光速より大きな速度で飛んでいる何かが、
私たちにはどう見えるか？」です。
仮に、「光が光っている」と仮定するなら、
速度C（光速）で飛んでいる光側から見た光も速度C（光速）で飛んでいる。
ただ、その光を私たち側から見ると、私たちはその光を
２重に重なった光として認識している訳です。
という事は、仮定に従えば、光に関して下図のように見えるはず。
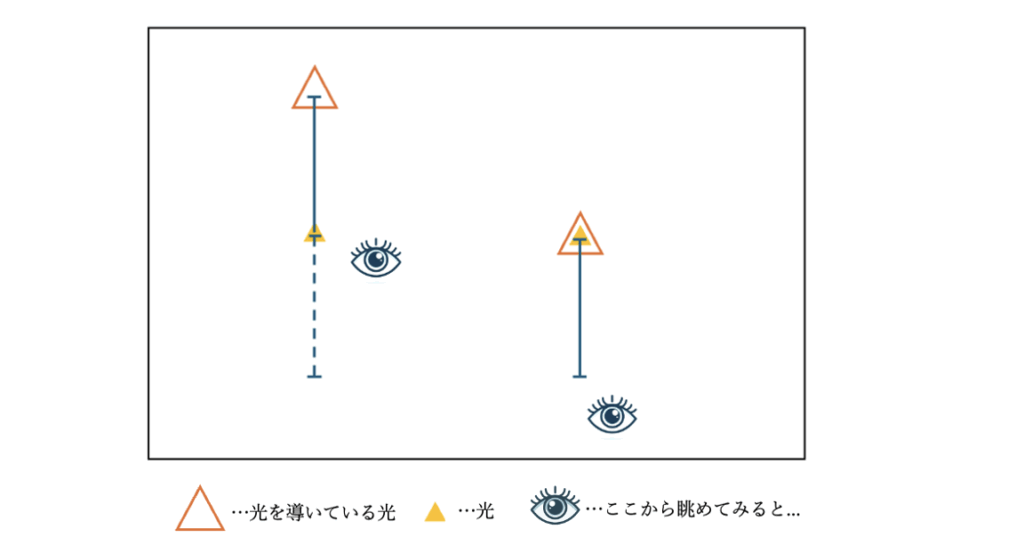
表現すると、こんな感じ。。。
とするならば、
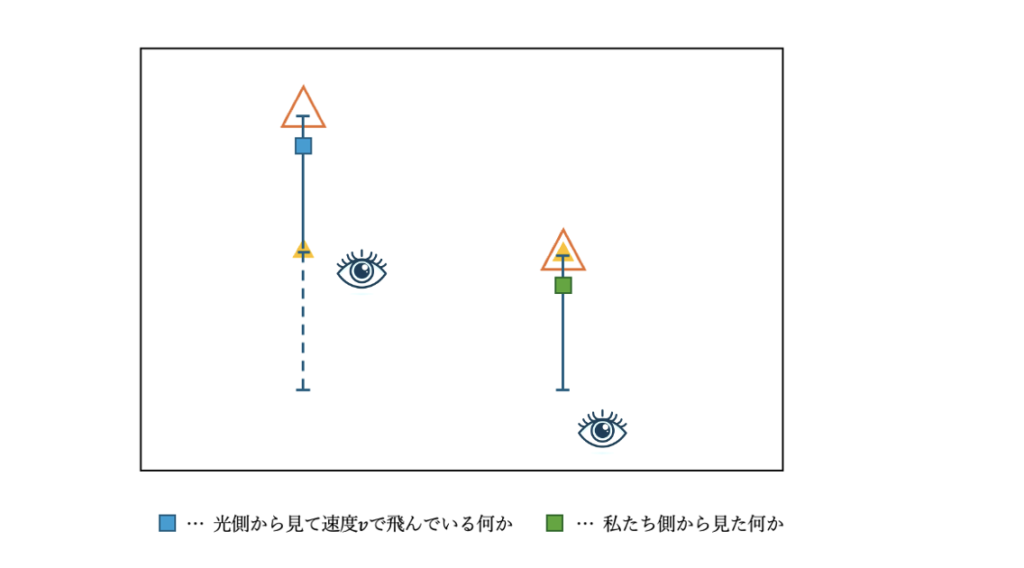
「光側から見て速度$v$ で飛んでいる何か（青の四角形）」が、
「私たち側から見ると、ここら辺（緑の四角形）」を飛んでいるかもしれない。。。
この「光側から見て速度$v$ で飛んでいる何か（青の四角形）」が、
「私たち側から見た何か（緑の四角形）」の位置を飛んでいる事があるとするなら、
次のように考える事が出来るのではないか？
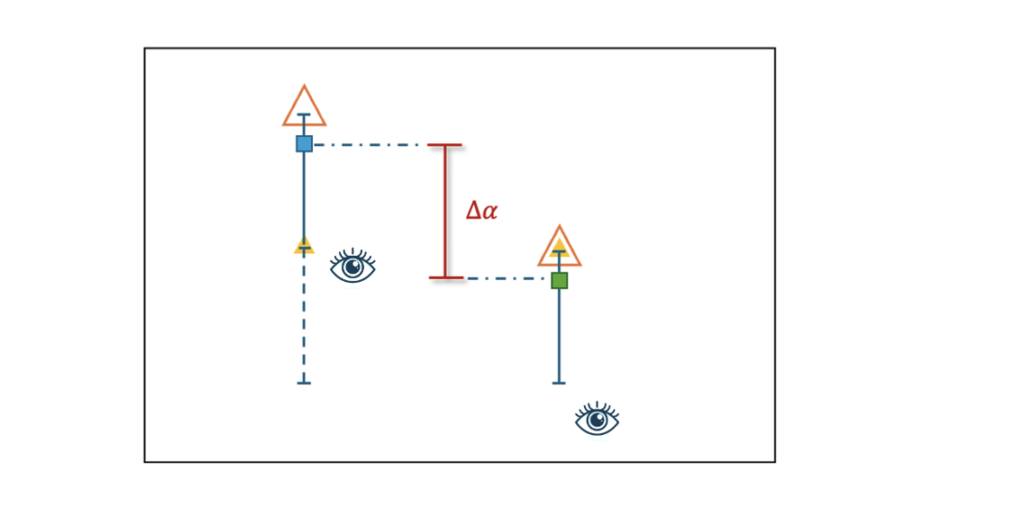
この、「光側から見て速度$v$ で飛んでいる何か（青の四角形）」が
「私たち側から見た何か（緑の四角形）」の位置にある時、
2つの位置に関してある一定の差があり、その差分を $\Delta\alpha$ とすれば、
「私たち側から見た何か（緑の四角形）」は
「光側から見て速度$v$で飛んでいる何か（青の四角形）」から
差分 $\Delta\alpha$ だけ後退しているように見える。
この時、「光側から見て速度$v$で飛んでいる何か（青の四角形）」と
「私たち側から見た何か（緑の四角形）」が同一のものであると言えれば、
その差分 $\Delta\alpha$ だけ「時が巻き戻っている」とみなして良いのでないか？
また、この $\Delta\alpha$ は計算によって求めることが出来る。。。
それでは、$\Delta\alpha$ を計算により求めてみよう。
計算にあたって次のような準備をする。
今、上記で示した「光側から見て速度$v$ で飛んでいる何か（青の四角形）」は、
光側から見た光を追い越してはいない。
従って、「光側から見て速度$v$ で飛んでいる何か（青の四角形）」の速度は
光側から見れば、光速を越えてはいない。
しかし、「光側から見て速度$v$ で飛んでいる何か（青の四角形）」は
私たち側から見れば、光の速さで飛んでいる光を追い越して存在している。
従って、この「光側から見て速度$v$ で飛んでいる何か（青の四角形）」の速度は、
私たち側から見れば、光速より大きな速度という事になる。
この時、私たち側から見た「青の四角形」の速度を$v_B$ としよう。
当然ながら、この速度 は光速より大きな値です。
また、「緑の四角形」の速度を$v_A$ としよう。
この$v_A$ は光速より小さな値としてとる。
何故なら、
「光側から見て速度$v$ で飛んでいる何か（青の四角形）」が、
「私たち側から見た何か（緑の四角形）」の位置を飛んでいる時、
つまり、「緑の四角形が、光速より小さな速度で飛んでいる時」を
対象とした議論であるため。
図示するとこんな感じ。。。
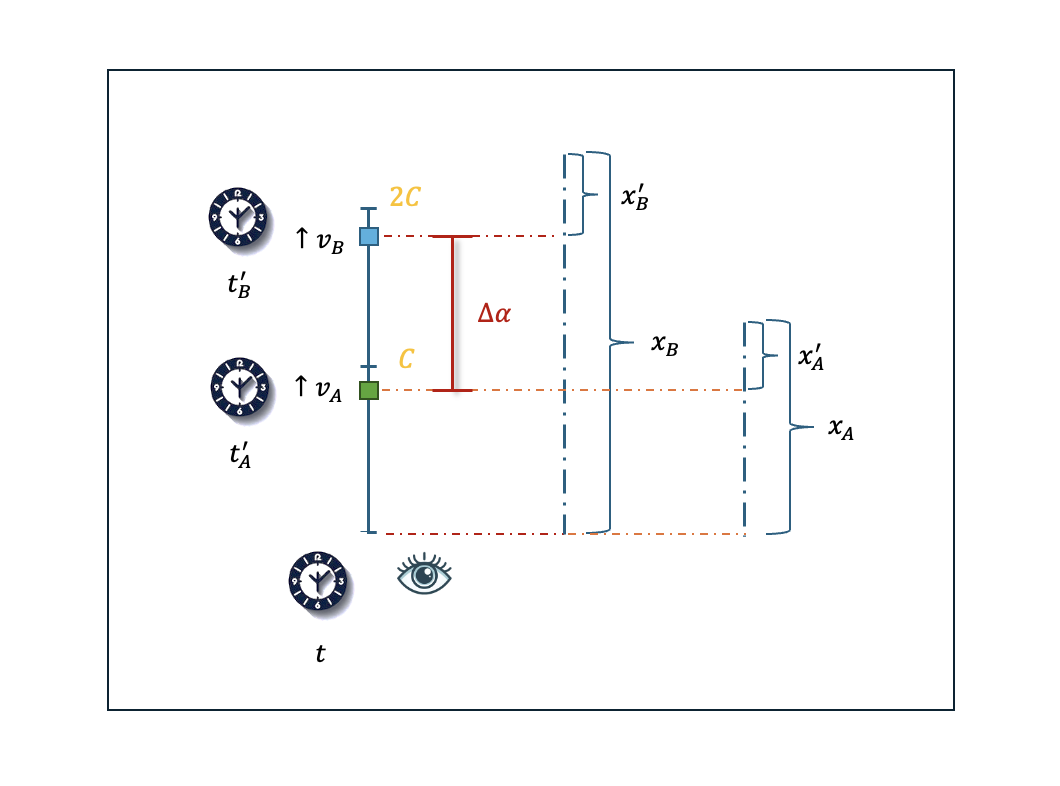
「青の四角形」に関わる方程式は、これ。
$x_B^\prime=\cfrac{x_B-v_Bt}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}$ $x_B=\cfrac{x_B^\prime+v_Bt_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}$
$t_B^\prime=\cfrac{t-\cfrac{v_B}{4c^2}x_B}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}$ $t=\cfrac{t_B^\prime+\cfrac{v_B}{4c^2}x_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}$
ただし、$c\leq{v_B}<2c$
「緑の四角形」に関わる方程式は、これ。
$x_A^\prime=\cfrac{x_A-v_At}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}$ $x_A=\cfrac{x_A^\prime+v_At_A^\prime}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}$
$t_A^\prime=\cfrac{t-\cfrac{v_A}{c^2}x_A}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}$ $t=\cfrac{t_A^\prime+\cfrac{v_A}{c^2}x_A^\prime}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}$
ただし、$0\leq{v_A}<c$
この時、「青の四角形」に関わる方程式と
「緑の四角形」に関わる方程式の間に共通項が一つだけある。
それは何かというと、時間 $t$ 。
何故かというと、同じ位置から
「青の四角形」と「緑の四角形」を眺めるため。
その、同一の時間 $t$ によって
「青の四角形」に関わる方程式と「緑の四角形」に関わる方程式を
組み合わせる事が出来るのではないか、というのが私の推理です。
ちょっと、簡略化してみた。
$x_A^\prime=0$ かつ $x_B^\prime=0$ の時の具体例。
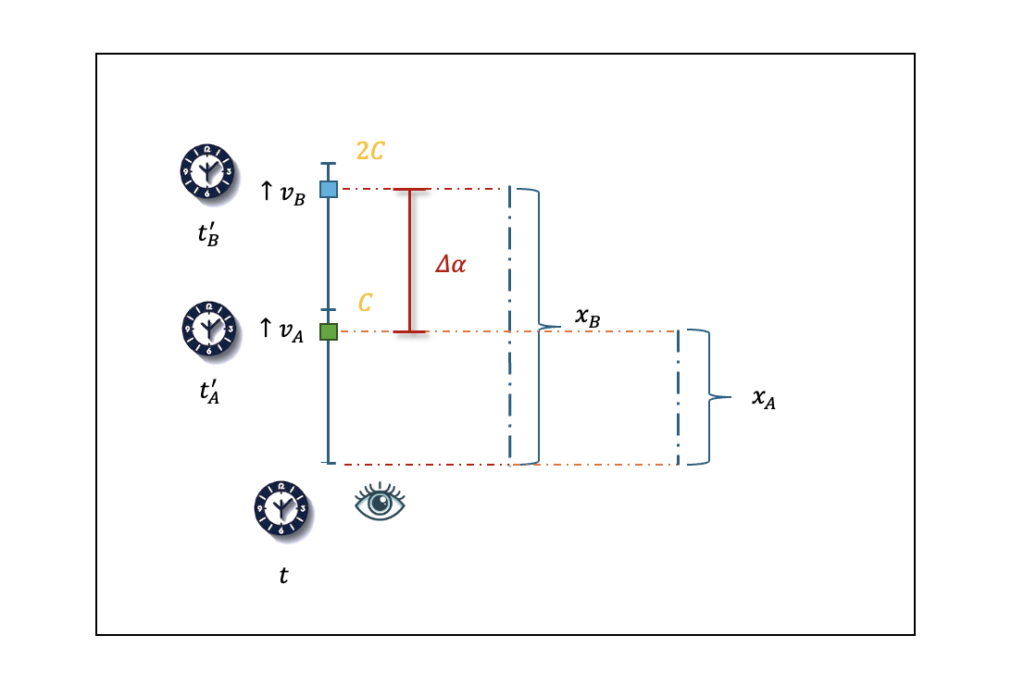
まずはこれで、$\Delta\alpha$ を求めてみよう。
$\Delta\alpha=x_B-x_A$ __①
この時、「青の四角形」に関わる方程式より
$x_B=\cfrac{x_B^\prime+v_Bt_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}$
今、$x_B^\prime=0$ より
$x_B=\cfrac{v_Bt_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}$
また、「緑の四角形」に関わる方程式より
$x_A=\cfrac{x_A^\prime+v_At_A^\prime}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}$
今、$x_A^\prime=0$ より
$x_A=\cfrac{v_At_A^\prime}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}$
この時、①に $x_B$、$x_A$ を代入し
$\Delta\alpha=x_B-x_A$
$=\cfrac{v_Bt_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}-\cfrac{v_At_A^\prime}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}$
この時、
$v_B=2\displaystyle\sqrt{\cfrac{{t_B^\prime}^2}{{t_A^\prime}^2}(v_A^2-c^2)+c^2}$ より （※1 補足あり）
$v_B^2=4\Big\lbrace \cfrac{{t_B^\prime}^2}{{t_A^\prime}^2}(v_A^2-c^2)+c^2 \Big\rbrace$
∴
$\Delta\alpha=\cfrac{v_Bt_B^\prime}{\displaystyle\sqrt{1-\cfrac{4\Big\lbrace \cfrac{{t_B^\prime}^2}{{t_A^\prime}^2}(v_A^2-c^2)+c^2 \Big\rbrace}{4c^2}}}-\cfrac{v_A{t_A}^\prime}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}$
$=\cfrac{v_Bt_B^\prime}{\displaystyle\sqrt{1-\cfrac{{t_B^\prime}^2(v_A^2-c^2)+{t_A^\prime}^2c^2}{{t_A^\prime}^2c^2}}}-\cfrac{v_At_A^\prime}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}$
$=\cfrac{v_Bt_B^\prime}{\displaystyle\sqrt{\cfrac{{t_A^\prime}^2c^2-{t_B^\prime}^2(v_A^2-c^2)-{t_A^\prime}^2c^2}{{t_A^\prime}^2c^2}}}-\cfrac{v_At_A^\prime}{\displaystyle{\sqrt{1-\cfrac{v_A^2}{c^2}}}}$
$=\cfrac{v_Bt_B^\prime}{\displaystyle\sqrt{\cfrac{{t_B^\prime}^2(c^2-v_A^2)}{{t_A^\prime}^2c^2}}}-\cfrac{v_At_A^\prime}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}$
$=\cfrac{v_Bt_B^\prime}{\cfrac{t_B^\prime}{t_A^\prime}\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}-\cfrac{v_At_A^\prime}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}$
$=\cfrac{\cfrac{t_A^\prime}{t_B^\prime}v_Bt_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}-\cfrac{v_At_A^\prime}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}$
$=\cfrac{v_Bt_A^\prime}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}-\cfrac{v_At_A^\prime}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}$
$=\cfrac{(v_B-v_A)t_A^\prime}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}$
別の視点で見ると、
$\Delta\alpha=x_B-x_A$ __❶
この時、「青の四角形」に関わる方程式より
$x_B=\cfrac{x_B^\prime+v_Bt_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}$
今、$x_B^\prime=0$ より
$x_B=\cfrac{v_Bt_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}$
また、「緑の四角形」に関わる方程式より
$x_A=\cfrac{x_A^\prime+v_At_A^\prime}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}$
今、$x_A^\prime=0$ より
$x_A=\cfrac{v_At_A^\prime}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}$
この時、❶に $x_B$、$x_A$ を代入して
$\Delta\alpha=x_B-x_A$
$=\cfrac{v_Bt_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}-\cfrac{v_At_A^\prime}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}$
この時、
$v_A=\displaystyle\sqrt{\cfrac{{t_A^\prime}^2}{{t_B^\prime}^2}(\cfrac{1}{4}v_B^2-c^2)+c^2}$ より （※2 補足あり）
$v_A^2=\cfrac{{t_A^\prime}^2}{{t_B^\prime}^2}(\cfrac{1}{4}v_B^2-c^2)+c^2$
∴
$\Delta\alpha=\cfrac{v_Bt_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}-\cfrac{v_At_A^\prime}{\displaystyle\sqrt{1-\cfrac{\cfrac{t_A^\prime}{t_B^\prime}( \cfrac{1}{4}v_B^2-c^2 )+c^2}{c^2}}}$
$=\cfrac{v_Bt_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}-\cfrac{v_At_A^\prime}{\displaystyle\sqrt{1-\cfrac{\cfrac{{t_A^\prime}^2}{{t_B^\prime}^2}( \cfrac{1}{4}v_B^2-c^2 )}{c^2}-1}}$
$=\cfrac{v_Bt_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}-\cfrac{v_At_A\prime}{\displaystyle\sqrt{\cfrac{-\cfrac{{t_A^\prime}^2}{{t_B^\prime}^2}( \cfrac{1}{4}v_B^2-c^2 )}{c^2}}}$
$=\cfrac{v_Bt_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}-\cfrac{v_At_A\prime}{\displaystyle\sqrt{\cfrac{\cfrac{{t_A^\prime}^2}{{t_B^\prime}^2}( c^2-\cfrac{1}{4}v_B^2 )}{c^2}}}$
$=\cfrac{v_Bt_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}-\cfrac{v_At_A^\prime}{\displaystyle\sqrt{\cfrac{{t_A^\prime}^2}{{t_B^\prime}^2}( 1-\cfrac{v_B^2}{4c^2} )}}$
$=\cfrac{v_Bt_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}-\cfrac{v_At_A^\prime}{\cfrac{t_A^\prime}{t_B^\prime}\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}$
$=\cfrac{v_Bt_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}-\cfrac{\cfrac{t_B^\prime}{t_A^\prime}v_At_A^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}$
$=\cfrac{v_Bt_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}-\cfrac{v_At_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}$
$=\cfrac{(v_B-v_A)t_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}$
以上より
$\Delta\alpha=\cfrac{(v_B-v_A)t_A^\prime}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}} or \cfrac{(v_B-v_A)t_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}$
この時 $\Delta\alpha$ は「青の四角形」が通った道のりの一部である事から、
この $\Delta\alpha$ を「青の四角形」の速度 $v_B$ で割る事で
「青の四角形」が $\Delta\alpha$ をどれだけの時間をかけて通過したのかが分かる。
従って、この「青の四角形」が $\Delta\alpha$ を通過した時間を $\Delta t$ とおけば、
$\Delta t=\Delta\alpha\div v_B$
$=\cfrac{\Delta\alpha}{v_B}$
$=\cfrac{(v_B-v_A)t_A^\prime}{v_B\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}} or \cfrac{(v_B-v_A)t_B^\prime}{v_B\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}$
またこの時、「青の四角形」と「緑の四角形」の間には
$\Delta t$ の時間差があり、もし「青の四角形」が「緑の四角形」の位置に
見えるとするならば、この$\Delta t$の時間差分だけ「時が巻き戻っている」
と言えるのではないか？
従って、この時
$x_A=v_B\times(T-\Delta t)$
$T$…「青の四角形」が図の位置に到達するまでの時間
$\Delta t$ …「青の四角形」の位置からの時間の巻き戻り分
と置け、計算すると
$x_A=v_B\times(T-\Delta t)$は
$T=\cfrac{t_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}$ また $\Delta t=\cfrac{(v_B-v_A)t_A^\prime}{v_B\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}$ or $\cfrac{(v_B-v_A)t_B^\prime}{v_B\sqrt{1-\cfrac{v_B^2}{4c^2}}}$ より
$x_A=v_B\times \Bigg\lbrace \cfrac{t_B^\prime}{\sqrt{1-\cfrac{v_B^2}{4c^2}}}-\cfrac{(v_B-v_A)t_B^\prime}{v_B\sqrt{1-\cfrac{v_B^2}{4c^2}}} \Bigg\rbrace$
※$\Delta t$に関して後者を利用
$x_A=\cfrac{v_Bt_B^\prime}{\sqrt{1-\cfrac{v_B^2}{4c^2}}}-\cfrac{(v_B-v_A)t_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}$
$x_A=\cfrac{v_Bt_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_B^2}{4c^2}}}-\cfrac{v_Bt_B^\prime}{\sqrt{1-\cfrac{v_B^2}{4c^2}}}+\cfrac{v_At_B^\prime}{\sqrt{1-\cfrac{v_B^2}{4c^2}}}$
$x_A=\cfrac{v_At_B^\prime}{\sqrt{1-\cfrac{v_B^2}{4c^2}}}$
この時、$v_B=2\sqrt{\cfrac{{t_B^\prime}^2}{{t_A^\prime}^2}(v_A^2-c^2)+c^2}$ より
$v_B^2=4\Bigg\lbrace \cfrac{{t_B^\prime}^2}{{t_A^\prime}^2}(v_A^2-c^2)+c^2 \Bigg\rbrace$
∴
$x_A=\cfrac{v_At_B^\prime}{\displaystyle\sqrt{1-\cfrac{4\Big\lbrace \cfrac{{t_B^\prime}^2}{{t_A^\prime}^2}(v_A^2-c^2)+c^2 \Big\rbrace}{4c^2}}}$
$=\cfrac{v_At_B^\prime}{\displaystyle\sqrt{1-\cfrac{\cfrac{{t_B^\prime}^2}{{t_A^\prime}^2}(v_A^2-c^2)+c^2}{c^2}}}$
$=\cfrac{v_At_B^\prime}{\displaystyle\sqrt{1-\cfrac{{t_B^\prime}^2v_A^2}{{t_A^\prime}^2c^2}+\cfrac{{t_B^\prime}^2c^2}{{t_A^\prime}^2c^2}-1}}$
$=\cfrac{v_At_B^\prime}{\displaystyle\sqrt{\cfrac{{t_B^\prime}^2}{{t_A^\prime}^2}(1-\cfrac{v_A^2}{c^2})}}$
$=\cfrac{v_At_B^\prime}{\cfrac{t_B^\prime}{t_A^\prime}\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}$
$=\cfrac{\cfrac{t_A^\prime}{t_B^\prime}v_At_B^\prime}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}$
∴
$x_A=\cfrac{v_At_A^\prime}{\displaystyle\sqrt{1-\cfrac{v_A^2}{c^2}}}$
この時、$x_A$は上記の方程式で満たされる事より
大意は示された。
これ、3つの前提条件が正しい事が必要。
つまり、3つの前提条件が正しい事が言えないと、妄想の可能性がある。
その3つの前提条件を示しておく。
1. 「光が光っている事」
2.「光の先を先行する何かが特殊相対性理論（改良版）の通りに動く事」
3.「光を先行する何か（青の四角形）がこちら側から見ると緑の四角形の位置にある事」
3年間で考えたのはここまで。。。
一般化までは至らずです。
